Gravi-Electromagnetismo en cinco dimensiones y cuerpos en movimiento en el área de la Galaxia
W. B. Belayev / D. Yu. Tsipenyuk-Center for relativity and Astrophysics, 185 Box, 194358, Sanct-Teresburg Russia
-General Physics Institute of the Russian Academy of Sciences, 38 Vavilova str., Moscow, 119991, Russia
Recibido: Agosto 31, 2004
En el modelo geométrico de Klein del espacio, la masa es la manifestación de las oscilaciones de las cargas cuantizadas en una compactada dimensión adicional. Nosotros analizamos el modelo en el cual las cuatro dimensiones del espacio-tiempo, para la masa y carga eléctrica de la trayectoria de la partícula, es desintegrada en cinco dimensiones en movimiento de la masas a lo largo de una linea geodésica nula y la trayectoria de la carga correspondiente a la intervalo similar al tiempo en un volumen 5D. Nosotros encontramos la relación entre el vector cinco-velocidad de la carga eléctrica y la masa. Este esquema considera muchas teorías mundiales. El enfoque considerado es aplicado al modelo de espacio tiempo rotante teniendo una simetría de esfera cuatri-dimensional. Una aparente propuesta fuerza adicional incluida en el espacio-tiempo 4D, debe tener explicación del efecto Pioneer. Nosotros analizamos también una posible parte de esta fuerza en conservación de la sustancia en el área de la galaxia.
Varias teorías, siendo estudiado el espacio-tiempo quinti-dimensional, estan fundamentadas en diferentes principios físicos. Una generalización de ka teoría específica de la relatividad para un espacio extendido G (R; ; S) con la métrica (+;-,-,-,-) ha sido propuesta y desarrollada en múltiples trabajos [1-8]. El modelo construido de espacio extendido (ESM, por sus siglas en inglés) permite la integración de las interacciones electromagnéticas y gravitacionales.
; S) con la métrica (+;-,-,-,-) ha sido propuesta y desarrollada en múltiples trabajos [1-8]. El modelo construido de espacio extendido (ESM, por sus siglas en inglés) permite la integración de las interacciones electromagnéticas y gravitacionales.
La peculiaridad el ESM es su estudio de la trayectoria de la partícula en 5D basada en la analogía entre el movimiento de la luz en une espacio curvado, en el marco de la relatividad general, y su movimiento en un medio con coeficiente de refracción mayor que la unidad [2,3,6]. En ESM la masa de la partícula es un componente del quinto vector energía-impulso-masa en el espacio G (R;;S). Con cambios de los marcos de coordenadas en el espacio, los campos eléctricos, gravitacionales y escalares son transformados los unos en los otros,
Como la quinta coordenada adicional en ESM es usada cuantitativamente, el cual ya existe en el espacio Minkowski (1+3)-dimensional M (T; ), con al coordenada de tiempo x0=ct, dodne c es la velocidad de la luz, t es el tiempo y las coordenadas x0, x1, x2, x3 definen en intervalo S:
El valor de S es conservado en la transformación común de Lorentz en el espacio Minkowski M(T; ) pero varía en turnos en el espacio extendido G (R; ; S). Así, el espacio Minkowski es un cono del espacio extendido.
En la teoría de gravedad 5D, iniciada por Nordstrom [9] y Kaluza [10], propuesta por el enfoque de Klein [11] sobre análisis del movimiento de la partícula, por ejemplo, en [12-15] requiere su trayectoria para se una linea geodésica nula en el espacio 5D. Se asegura que una partícula que no tenga masa de reposo en el espacio 4D Minkowski la tenga en 5D. El otro enfoque de la cinemática en un espacio 5D usa una descripción del movimiento de las partículas, las cuales pueden ser estacionarias en este espacio y tener un masa resultante diferente de cero. Y su trayectoria es determinado por el intervalo similar al tiempo.
En consideración del modelo integrado del electromagnetismo y gravedad, nosotros podemos emperezar a tomar en cuenta a partir de la compactificación de Klein fundada en la suposición de que la carga eléctrica y la masa de lo observado en una partícula 4D tiene diferentes lineas mundiales en un espacio 5D. Por ello, nosotros suponemos cualquier partícula que tenga una masa resultante en 4D a contener una combinación de cargas eléctricas. La masa en movimiento conforma el intervalo nulo, es decir:
donde el tercer elemento (X^i m) son coordenadas de masa y el primer producto (Gij(xm)) es un tensor de métrica de un espacio 5D, que es función de dichas coordenadas. Por el contrario, la carga eléctrica tiene una trayectoria con un elemento de linea.
donde x^i son las coordenadas de carga.
Luego, lineas mundiales de la masa de la partícula en intersectos 5D correspondiendo a las lineas mundiales de la carga eléctrica y, a la inversa, la trayectoria de esta carga eléctrica es un set de los puntos relacionados con trayectorias de las correspondientes masas. Este enfoque nos llevo a proponer, por Everett [21-23], concepciones de varios mundos fundados en la teoría del quantum.
Toquemos relaciones con el presente esquema para el principio antrópico. Nuestra percepción del ambiente surge por medios electromagnéticos pero nosotros no podemos sentir gravedad directa. Esto puede se tomado en cuenta para una suposición de que para ser una masa exacta, no se mueven cargas eléctricas a lo largo del paso nulo en 5D. Es este caso nosotros podemos sostener que un modelo del espacio 5D con una masa resultante diferente de cero de la partícula y apropiados intervalos similares a tiempo describen la traza eletromagnética de las masas, los cuales estan relacionados consecutivamente con la linea mundial correspondiente a la combinación de cargas eléctricas. La velocidad de la luz en una dimensión extra en un marco de coordenadas de carga o sistema de cargas, siendo su fuente asumida como nula.
Componentes de la velocidad de masa denotada como u^i m = dx^i m/dse forman un quinto vector. Teniendo primero 4 componentes de un vector cinco-velocidad de carga u^i correspondiendo al intervalo (tercera ecuación) iguala u^i m = u^i proporciona coincidencia local de las coordenadas de la masa y carga en 4D. Dividiendo la ecuación 2 con d s^2 e nosotros obtenemos:
En este punto la velocidad de la masa a lo largo de quinta coordenada puede ser
donde e = +-1; i,j =/ 4. Los valores opuestos de e conforman la materia y antimateria. Para el espacio extendido de Minkowski del espacio, tenemos:
Apliquemos conceptos considerados para el análisis del ejemplo métrico de un espacio 5D con aquel vector base que es el quinto de ellos y no es ortogonal a los otros, con estas bases del espacio incluido. El modelo cosmológico con movimiento de la materia a través de la quinta coordenada basada en si mismo en métricas conformes a esta propiedad han sido estudiados en [20]. Nosotros analizamos el espacio-tiempo incluido en un espacio esférico cuatri-dimensional, con coordenadas
para ser traducido en el marco ortogonal por las transformaciones
Este espacio se supone que gira y la métrica toma la forma:
dodne B(a) es dependiente del coeficiente a. En concordancia con el enfoque considerado con ds>0 de acuerdo con el movimiento de la traza de la partícula electromagnética.
En [20] la ecuación de la linea geodésica fue escrita en la forma
Para métrica zeroth (ecuación anterior a esta), el primero y cuarto componente de estas ecuaciones con coordenadas de tipo convencional (u^1=u^2=u^3=0) produce
La solución de este sistema debe ser compatible con el set métrico citado anteriormente (zeroth) por la condición métrica:
Cuya solución va a ser
donde e toma valores los valores 1 y -1. Correspondiendo al quinto componente de la 5-velocidad de la masa, tenemos lo siguiente:
Nosotros nos percatamos que esta ecuación con otros cuatro componentes de u^i m don puede dar un valor nulo a las geodésicas de la partícula de la masa pero eso es solo la velocidad de la pasa en cada punto de carga geodésica,
Un marco considerado es transformado a las coordenadas
teniendo solo simetría 3D por las expresiones
Esta aceleración adicional satisface la restricción
, donde R es el radio de la galaxia y Vsw es la velocidad del viento solar [28]. Esto sigue de esto que si el efecto Pioneer se expande por todo el área de la galaxia, esto nos lleva a la conservación de la materia dentro de los límites del cinturón de la galaxia.
Referencias
1] D.Yu. Tsipenyuk, V.A. Andreev, Krattkie Soobstcheniya po Fizike (Bulletin of Lebedev Physics Institute (Russian Academy of Sciences)) 6, 23{34, (2000); arXiv: gr-qc/0106093.
[2] D.Yu. Tsipenyuk, V.A. Andreev, Issledovano v Rossii, 60, (1999) (in Russian); http://zhurnal.ape.relarn.ru/articles/1999/060.pdf
[3] D.Yu. Tsipenyuk, Gravitation and Cosmology, Vol. 7, No.4(28), 336{338, (2001); arXiv: physics/0203017.
[4] D.Yu. Tsipenyuk, Krattkie Soobstcheniya po Fizike (Bulletin of Lebedev Physics Institute (Russian Academy of Sciences)) 7, 39{49, (2001); arXiv: physics/0107007.
[5] D.Yu. Tsipenyuk, V.A. Andreev, Krattkie Soob- stcheniya po Fizike(Bulletin of Lebedev Physics Institute (Russian Academy of Sciences)) 6, 3{15, (2002); arXiv: physics/0302006.
[6] D.Yu. Tsipenyuk, Issledovano v Rossii 81, 907{916, (2001)(in Russian); http://zhurnal.ape.relarn.ru/articles/2001/081.pdf.
[7] D.Yu. Tsipenyuk, V.A. Andreev, \Electrodynamics in Extended Space," preprint IOFAN 9, Moscow, (1999)(in Russian).
[8] D.Yu. Tsipenyuk, V.A. Andreev, \Gravitational effects in Extended Space," preprint IOFAN 4,
Moscow,(2001)(in Russian).
[9] G. Nordstrom, Phyz. Zeitschr.1, 504 (1914) (in German).
[10] T. Kaluza, Sitz. Preuss. Akad. Wiss. Phys. Math. K1, 966 (1921) (in German).
[11] O. Klein Z. Phys. 37, 895 (1926).
[12] J. Van Dongen, arXiv: gr-qc/0009087.
[13] P.S. Wesson, S.S. Seahra, Gen. Rel. Grav., 33, 1731 (2001); arXiv: gr-qc/0105041.
[14] W.B. Belayev, \Extra force in Kaluza-Klein gravity theory," Invited talk at \Gravitation, Cosmology and Relativistic Astrophysics" (Kharkiv, Ukraine, June 23-27, 2003); arXiv: gr-qc/0308076.
[15] P.S. Wesson, Gen. Rel. Grav. 35, 307 (2001); arXiv: gr-qc/0302092.
[16] J.M. Overduin, P.S.Wesson, Phus. Rept., 283, 303 (1997); arXiv: gr-qc/9805018.
[17] J. Ponce de Leon, Phys. Lett. B 523, 311 (2001); arXiv: gr-qc/0110063.
[18] R. Maartens, \Geometry and dynamics of the brane-world," invited talk at EREs2000, Spanish Relativity Meeting; arXiv: gr-qc/0101059.
[19] F. Dahia, E.M. Monte, C. Romero, Mod. Phys. Lett. A 25, 1173, (2003); arXiv: gr-qc/0303044.
[20] W.B. Belayev, Spactime and Substance 7, 63 (2001); arXiv: gr-qc/0110099.
[21] B.S. DeWitt, R. N. Graham, \The many-worlds Interpretation of Quantum Mechanics," eds. R. N. Graham, Princeton Series in Physics, Princeton University Press (1973).
[22] F.J. Tipler, in \Quantum Concepts of Space and Time," eds R. Penrose and C. Isham, Oxford University Press (1986).
[23] D. Bohm, B.J. Hiley, \The Undivided Universe," Routledge Press, London, 1993.
[24] G.C. McVittie, \General Relativity and Cosmology" Chapman and Half Ltd., London, 1956. (Russian translation: G.C. Mac-Vitti, \General Relativity and Cosmology," IIL, Moskow, 1961.)
[25] J.D. Anderson, P.A. Laing, E.L. Lau, A.S. Liu, M.M. Nieto, S.G. Turushev, Phys. Rev. Lett. 81, 2858 (1998); arXiv: gr-qc/9808081.
[26] S.G. Turushev, J.D. Anderson, P.A. Laing, E.L. Lau, A.S. Liu, M.M. Nieto, \The apparent anomalous, weak, long-range acceleration of Pioneer 10 and 11," XXXIV-th Rencontres de Morion Meeting on Gravitational Waves and Experimental Gravity 1999, Les Arcs, Savoi, France; arXiv: gr-qc/9903024.
[27] J.D. Anderson, P.A. Laing, E.L. Lau, A.S. Liu, M.M. Nieto, S.G. Turushev, Phys. Rev. D 65, 082004 (2002); arXiv: gr-qc/0104064.
[28] K. Tren cevski, unpublished data, 2004.
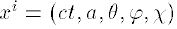
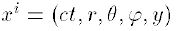
No hay comentarios.:
Publicar un comentario